The SCiFI Research Team pursues diverse projects at the interface of Financial Mathematics, Stochastic Modeling and Machine Learning. Our work has been supported by the National Science Foundation (Algorithms for Modern Power Systems and Computational Data-Enabled Science and Engineering programs run by Division of Mathematical Sciences) and Casualty Actuarial Society.

Stochastic Games
 

Competitive markets prominently feature strategic participant behavior. We are interested in modeling the resulting dynamic equilibrium using continuous-time stochastic models. A particular emphasis is on non-zero-sum games which arise naturally in Cournot-type competition.

Recent projects investigated R& D games where players compete for technological advantage, mean-field game among exhaustible resource producers, multi-stage timing games for capacity investment, and stationary switching games displayed in the figure below. The latter model allowed for explicit computation of the emergent macroscopic market equilibrium (which is a one-memory Markov chain).

Stochastic Control Applications in Energy Markets
 

We develop simulation-based computational algorithms for stochastic control. This work is geared towards energy applications, including valuation of natural gas storage facilities and battery management in electricity microgrids. Our Dynamic Emulation Algorithm weaves together the Regression Monte Carlo approach, nonparametric functional approximators, and experimental design strategies. DEA unifies existing Monte Carlo frameworks across a range of stochastic settings, including optimal stopping, optimal switching and impulse control.

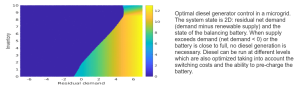
Emulation of Stochastic Simulators

We investigate efficient methods for emulation of stochastic experiments, viewed as stochastic black-boxes. This forms a building block for a variety of applications, such as American Option pricing, illustrated below. Compared to the well-studied surrogates of deterministic experiments, stochasticity requires handling of the underlying noise, which in practical settings is often non-Gaussian, heteroskedastic and with low signal-to-noise ratio. We have developed and benchmarked a suite of emulation and design methods, ranging from t-Processes, to Binomial Gaussian Processes to handle replicated designs. Our ongoing research programme transcends statistics, stochastics and control.

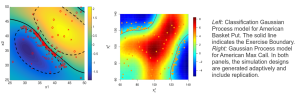
New Paradigms for Stochastic Root-/Contour-Finding Problems
 

In 1-D, solving an optimal stopping problem is equivalent to a sequence of Stochastic Root Finding Problems. We seek efficient Sequential Design strategies for the corresponding simulation experiments that directly optimize the information gain related to the SRFP task, rather than the typical approach that optimizes information collection for the auxiliary regression problem. To this end, we explore new ideas coming from the Learning literature, in particular the Probabilistic Bisection Algorithm. The PBA performs root finding based on knowledge acquired from noisy oracle replies. To make PBA applicable in a practical context, we consider the generalized PBA setting (G-PBA) where the statistical distribution of the oracle is unknown and location-dependent, so that model inference and Bayesian knowledge updating must be performed simultaneously. We have investigated both local G-PBAs that infer oracle accuracy through repeated queries at the same 'x'-location, and spatial G-PBA that leverage the spatial structure using a non-parametric statistical surrogate for the underlying logistic regression step. Connecting the PBA with the Gaussian Regression framework, we have developed sampling policies that adaptively balance learning the oracle distribution and learning the root.

Random Field Models for Mortality Surfaces

Estimation and forecasting of mortality rates is a key task in life insurance. We are developing new statistical frameworks that bring modern uncertainty quantification concepts to this domain. Our proposed use of Gaussian Process models offers a flexible, hierarchical paradigm for smoothing raw mortality experience, inferring mortality improvement rates, and generating stochastic scenarios of future mortality. A key benefit is a model-consistent output of credible bands around historical/current mortality rates, credible bands of mortality improvement rates, and credible intervals for value of actuarial products such as life annuities. Presently, we are investigating multi-population models, as well as advanced spatial covariance structures to capture cohort and international longevity trends.

Limit Order Books on the Mesoscale

For optimal execution and market making purposes, one generally wishes to aggregate high-frequency (sub-second) limit order book data into the scheduling time-scale of 1-10 minutes. This is also the appropriate scale for defining price impact, information leakage and book resilience. We are investigating LOB behavior on this meso-scale, especially the link between limit order flow, executed trade and price formation.

Media Coverage of our Research/Publicly Available Video Recordings

1/4/2024 Equitably Decarbonizing California (UCSB Current): California Climate Action project on renewables, electrification and climate resilience (2023-- present)

10/12/2023 Machine Learning Surrogates for Parametric and Adaptive Optimal Execution (SIAM/Youtube): hourlong recording of research webinar for SIAM Activity Group on Financial Mathematics

4/26/2023 Machine Learning for Optimal Stopping Problems (Fields Institute/Youtube): hourlong recording of research seminar at U of Toronto, Canada

10/13/2022 Striving for Inclusion (UCSB Current): NSF S-STEM project on supporting low-income UGs pursuing Data Science (2022--present)

4/21/2022 Probabilistic Modeling of Renewable Energy Generation (UCSB/Youtube): 80-minute research seminar at Institute for Energy Efficiency, UCSB

5/22/2022 Diving into Data (UCSB Current):  NSF HDR project on data science capstones (2020-2023)

7/28/2021 KZSB AM1290 About Education (CSUCI Presents) : Radio interview loosely covering our ARPA-E PERFORM project

3/23/2021 Uncertain Energy (UCSB Current): ARPA-E PERFORM project on risk management and statistical modeling of renewables (2020-2024)

5/29/2020 Panel discussion on Energy Markets and Quantitative Modeling (SIAM/Youtube)

3/17/2020 Gearing Up for Data Science (UCSB Current): NSF HDR project on data science capstones (2020--2023)

1/23/2020 Multi-population Longevity Models (Society of Actuaries Podcast): our work with Nhan Huynh on multi-population modeling of mortality surfaces using Gaussian processes